Exponential Functions
Math Class
Hello, my name is Alex Heinrich, and this is my algebra reflection. This year in algebra class we started a whole new set of linear and non-linear equations and graphing. The one that was hardest for me was exponential functions that is in the beginning. But as we learned more and more about it, it became easier for me to do. This was not only because I tried harder, it was also because Mrs. Vazquez and a couple of people at my table helped me understand this. They mentored me until I got it and when I got something wrong they explained it to me and told me where I messed up. So, therefore my claim is that I grew in graphing and solving exponential functions.
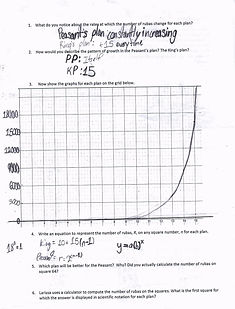
My first artifact is king and peasants problem. This is an artifact from the exponential functions unit. In this problem the peasant saves the kings daughter and the peasant can choose how much gold he wants. So the peasant says there are 64 squares on a chess board. You put one ruba ($100) on the first square, then you will put twice as many on the next square until all the 64th square and I will get all the ruba’s on the 64th square. So the peasants equation for the peasants plan is R=2^ (N-1). N stands for the number of squares it has advanced from one and R stands for the number of total Ruba’s that the peasant gets. So before we get into the major details let me explain some terms. An exponential functions is a type of non-linear equation that has an exponential growth or decay factor. What this means is that x is multiplied by the exponent to equal y, and there may be other things before solving y that you must do. Next is a growth rate. A growth rate is defined as a rate in which the exponential function produces a positive rate in which it plot points. Meaning that as the x-value continues, the y-value gets bigger. This artifact shows growth because I was able to graph the exponential function on the graph that Mrs. Vazquez provided us with. So the real question we had to answer was what is on square 64? So that equation looks like 2^ (64-1) which when you put into a calculator equals 9.223372037e18 which the e18 means that e=10 and 18 is e’s exponential value. So that would look like 10^18 which equals 1,000,000,000,000,000,000 and if that number isn’t high enough then you have to multiply it by 9.223372037 which eventually comes out to 9,223,372,037,000,000,000. That is 9 plus some quintillion, that is also 10^18. That is a big number I would love to be that peasant right now. This proves that I grew in exponential functions because I just explained the science behind exponential functions in a very descriptive way. Now for my 2nd artifact.
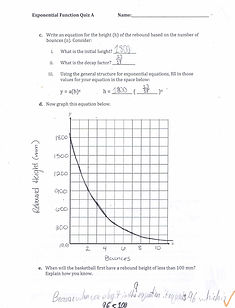
My 2nd artifact would be the exponential functions test. The reason that this is one of my artifacts is because I got a 10/10 on it. This was right after the peasant problem that we did in class. The test included questions where we had to graph the decay factor of a real world situation. This was especially hard for me because I wasn’t very good at graphing these things because I have a problem unclean lines. When I graphed this it took a couple of tries but I eventually got it. The question was talking about the required bounce height of a FIBA basketball. FIBA stands for International Basketball Federation. It said that if a FIBA basketball is dropped from 1800mm then it must bounce back up to 1300mm. This is a decay rate because the slope would be 13/18<1 but 13/18>0. I learned what a base value, and what a decay rate was. A base value that is multiplied by itself based off the exponent. It looks like this f(x)=b^x, where b is the base value and x is the exponent. A decay rate is when b<1, but b>0. Meaning that as the x-value rises, the y-value gets smaller, therefore causing it to have a negative slope or decay rate. The reason that this artifact shows grow is because if I was able to get a 100% on the quiz then I have to know how to solve and graph an exponential function. Now for my conclusion.
How do these prove that you grew in graphing and understanding exponential functions? Well my first artifact was the king and peasants problem. This artifact showed growth because I was able to solve this problem and I was able to explain it on this reflection. If I truly understand this then you should be able to see that I have grown in this topic. My 2nd artifact was the exponential functions unit test. This artifact proves growth because I got a 100% because I understood how exponential functions really worked. On the unit test you can find that I graphed everything correctly and I filled out the table on the front with everything being correct. This proves that I grew in graphing and solving exponential functions because I was able to get a 100% on the quiz. So what? Well to remind you my claim was that I grew in graphing and solving exponential functions. All of my artifacts support this claim so therefore my artifacts should convince you of my growth. I will need to continue to use these skills for the rest of my career at STEM and in the far future to accomplish my goal of maybe becoming a pilot.